AB and AC are two chords of a circle such that AB = 2AC. If distances of AB and AC from the centre are 3 cm and 6 cm respectively, find the area of circle. (Assume π =3)
- Home
- Math
- All Questions
Answer: 135 cm2
Step by Step Explanation: - Take a look at the representative image below:
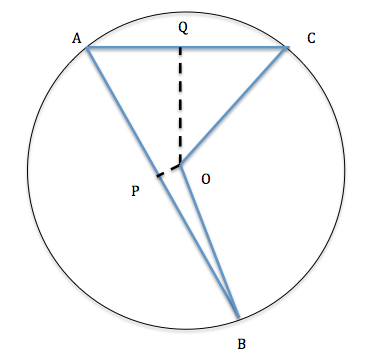
We are told that AB = 2AC.
Also, if the perpendicular from O to AC meets the chord at Q, then OQ = 6 cm.
Similarly, OP = 3 cm. - As the perpendicular from the centre on the chord bisects the chord, OQ bisects AC, and OP bisects AB.
From the earlier relation AB = 2AC.
Therefore, BP = 2CQ
Let us assume CQ = x.
Then, BP = 2x - Now consider ΔOQC,
OC = r, the radius of the circle, and OQ = 6 cm
As, the distance of a chord from the centre is always the perpendicular distance. ΔOQC is a right-angled triangle.
By using pythagoras theorum, OQ2 + CQ2 = r2
62 + x2 = r2
or, 36 + x2 = r2 ------(1) - Similarly, ΔOPB is a right-angled triangle,
OP2 + BP2 = r2
32 + (2x)2 = r2
or, 9 + 4x2 = r2 ------(2) - Subtracting equation (1) from equation (2), we get:
(9 - 36) + (4x2 - x2) = 0
or, 3x2 = 27
or, x2 = - On substituting x2 = in equation (1), we get:
36 + = r2
or, r2 = = - Therefore, area of the circle = πr2 = 3 × = 135 cm2

 USA
USA
