A spherical balloon of radius ^@ 15 ^@ feet subtends an angle ^@ 60^\circ ^@ at the eye of an observer. If the angle of elevation of its center is ^@ 45^\circ,^@ find the height of the center of the balloon.
Answer:
^@ 15 \sqrt{ 2 } \text{ feet } ^@
- The following picture shows the observer at point ^@ A,^@ observing a balloon.
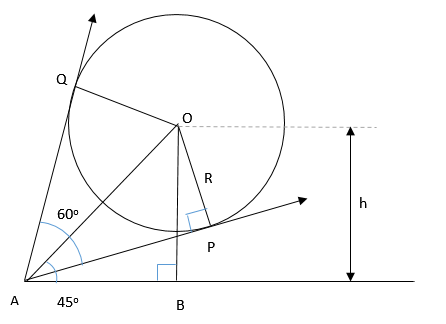
- Let's assume the height of the center of the balloon to be ^@ h, ^@ therefore ^@ OB = h ^@
Also, assume the distance of center of the balloon from observer to be ^@ D, ^@ therefore ^@ OA = D ^@ - For triangle ^@\triangle OAP, ^@
^@ \begin{align} & sin \angle OAP = \dfrac{ R } { D } \\ \implies & \dfrac{ sin 60^\circ } { 2 } = \dfrac{ R } { D } \\ \implies & sin 30^\circ = \dfrac{ R } { D } \\ \implies & \dfrac{ 1 }{ 2 } = \dfrac{ R }{ D} \\ \implies & D = 2R && \ldots (1) \end{align} ^@ - For ^@ \triangle AOB, ^@
^@ \begin{align} & sin \angle OAB = \dfrac{ h } { D } \\ \implies & sin 45^\circ = \dfrac{ h } { D } \\ \implies & { \dfrac{ 1 } { \sqrt{ 2 } }}^\circ = \dfrac{ h } { D } \\ \implies & D = \sqrt{ 2 } h && \ldots (2) \end{align}^@ - On equating two values of ^@ D ^@ from equation ^@(1)^@ and ^@(2),^@
^@\begin{align} & \sqrt{ 2 }h = 2R \\ \implies & h = R \sqrt{ 2 } \\ \implies & h = 15 \sqrt{ 2 } \text{ feet } \end{align} ^@
 USA
USA
